INTEGRAL TENTU (BAGIAN 1)

INTEGRAL TENTU - PENGANTAR LUASAN

Luas merupakan dasar untuk pembahasan integral tentu khususnya luas poligon, baik poligon dalam maupun poligon luar yang dapat dibuat pada bidang datar, didasarkan atas rumus luas persegi panjang.

LUAS MENURUT POLIGON DALAM

Sebagai contoh, akan dicari L (P) Luas Daerah datatr yang dibatasi oleh kurva y = f(x) =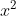 $x^{2}$ , sumbu -x, garis x = 0 dan x = 2. Pertama dipartisikan selang $0\leq x\leq 2$ atas selang bagian yang sama dengan panjang $\Delta x = \frac{2}{n}$ , dan memakai titik-titik:

$0 = x_{0}< x_{1 }< x_{2}< ...< x_{n}-1< x_{n}=2 sehingga:$

$x_{0} = 0$

$x_{1} = 0 + \Delta x = \frac{2}{n}= 1 .\frac {2}{n}$

$x_{2} = 0 + 2\Delta x = \frac{4}{n}= 2 .\frac {2}{n}$

$x_{3} = 0 + 3\Delta x = \frac{6}{n}= 3 .\frac {2}{n}$

$x_{n} = 0 + n\Delta x = n(\frac{2}{n}) = 2$

Pada gambar tampak bahwa $L(P)_{dalam} < L (P)_{luar}$

Luas poligon dalam:

$L(P)_{dalam} = f(x_{0})\Delta x + f(x_{1})\Delta x + f(x_{2})\Delta x +...+ f(x_{n-1})\Delta x$

$L(P)_{dalam} = (0^{2}) (\frac{2}{n})+ (1(\frac{2}{n}))^{2}\left ( \frac{2}{n} \right )+...+ (n-1)(\frac{2}{n})^{2}(\frac{2}{n})$

$= (\frac{2}{n})^{3} (0^{2}+1^{2}+2^{2}+...+(n-1)^{2})$

$= (\frac{2}{n})\sum_{i=0}^{n-1}i^{2}$

$= (\frac{2}{n})^{3}\left ( \frac{1}{6}(n-1) \right )(n)(2n-1)$

$= \frac{8}{3}-\frac{4}{n}+\frac{4}{3n^{2}}$

Sehingga,

$\displaystyle \lim_{ n\to \ \infty } L (P_{dalam})= \displaystyle \lim_{n \to \infty } (\frac{8}{3}-\frac{4}{n}+\frac{4}{3n^{2}})=\frac{8}{3}$

LUAS POLIGON LUAR

$L(P)_{luar} = f(x_{1})\Delta x + f(x_{2})\Delta x + f(x_{3})\Delta x +...+ f(x_{n})\Delta x$

$= (1(\frac{2}{n})^{2} (\frac{2}{n})+ \left ( 2(\frac{2}{n}) \right )^{2} (\frac{2}{n})+...+(n (\frac{2}{n})^{2} (\frac{2}{n})$

$= (\frac{2}{n})^{3}(1^{2}+2^{2}+3^{2}+...+ n^{2})$

$= (\frac{2}{n})\sum_{i=1}^{n}i^{2}$

$= (\frac{2}{n})^{3} (\frac{1}{6n}(n+1)(2n+1))$

$= \frac{8}{3}+\frac{4}{n}+\frac{4}{3n^{2}}$

Sehingga,

$\displaystyle \lim_{ n\to \ \infty } L (P_{luar})= \displaystyle \lim_{n \to \infty } (\frac{8}{3}+\frac{4}{n}+\frac{4}{3n^{2}})=\frac{8}{3}$

Berdasarkan Teorema Apit $L (P_{dalam})< L(P)< L (P_{luar})$ didapat $L(P) = \frac{8}{3}$

INTEGRAL TENTU (RIEMAN)

Pada lambang $\int_{a}^{b} f (x)dx,$ a disebut batas bawah dan b disebut batas atas dari integral tersebut.

Dalam definisi $\int_{a}^{b} f (x)dx,$ secara implisir kita menganggap bahwa $a< b$ . Menghilangkan batasan tersebut dengan definisi-definisi berikut:

CONTOH SOAL

Hitunglah luas poligon yang dibatasi oleh kurva $y = \frac{1}{2}$ x, sumbu x, garis x = 2 dan x = 4 , jika daerah poligon tersebut dibagi atas 5 poligon bagian yang sama.

penyelesaian:

Karena selang (2,5) dopartisi atas 5 selang bagian yang sama, maka $\Delta x = \frac{(4-2)}{5} = \frac{2}{5} , dan$

$x_{0}=2$

$x_{1}=2 + 1 \Delta x = 2 + \frac{2}{5} = \frac{12}{5}$

$x_{2}=2 + 2 \Delta x = 2 + \frac{4}{5} = \frac{14}{5}$

$x_{3}=2 + 3 \Delta x = 2 + \frac{6}{5} = \frac{16}{5}$

$x_{4}=2 + 4 \Delta x = 2 + \frac{8}{5} = \frac{18}{5}$

$x_{5}=2 + 5 \Delta x = 2 + \frac{10}{5} = \frac{20}{5} =4$

Luas poligon dalam

$L(P_{dalam})= f(x0)\Delta x + f(x1)\Delta x + f(x2)\Delta x+ + f(x3)\Delta x + f(x4)\Delta x$

$= \left ( \frac{1}{2} \right )(2)\left ( \frac{2}{5} \right )+\left ( \frac{1}{2} \right )\left ( \frac{12}{5} \right )\left ( \frac{2}{5} \right )+\left ( \frac{1}{2} \right )\left ( \frac{14}{5} \right )+\left ( \frac{1}{2} \right )\left ( \frac{16}{5} \right )\left ( \frac{2}{5} \right )+\left ( \frac{1}{2} \right )\left ( \frac{18}{5} \right )\left ( \frac{2}{5} \right )$

$= \left ( \frac{12}{5} \right ) +\left ( \frac{14}{5} \right )+\left ( \frac{18}{25} \right )+\left ( \frac{18}{25} \right )+\left ( \frac{20}{25} \right )$